Page 11
Sequences (Arithmetic and Geometric)
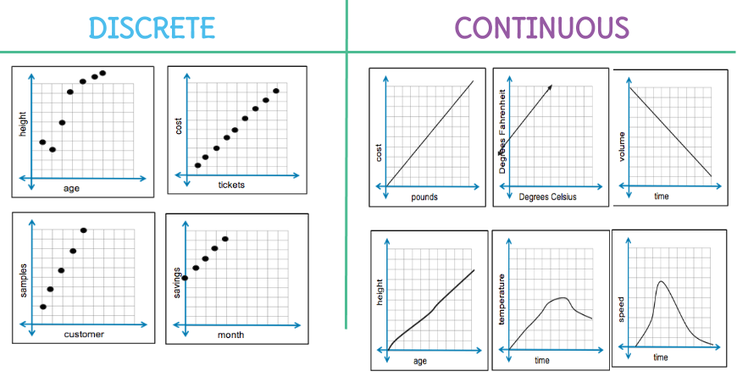
Discrete vs. Continuous Functions
Sequences are discrete functions because the domain is only natural numbers (positive integers).
If the graph of f(x) is the discrete function below, there is a definite value of f(1) and f(2), but f(1.5) does not exist.
Continuous functions have a domain of all real numbers (positive, negative, integers, fractions, zero).
If the graph of g(x) is the continuous function below, there is a definite value of g(1), g(-1), g(0), g(1.5), g(1.328947), etc.
If the graph of f(x) is the discrete function below, there is a definite value of f(1) and f(2), but f(1.5) does not exist.
Continuous functions have a domain of all real numbers (positive, negative, integers, fractions, zero).
If the graph of g(x) is the continuous function below, there is a definite value of g(1), g(-1), g(0), g(1.5), g(1.328947), etc.
|
|
|
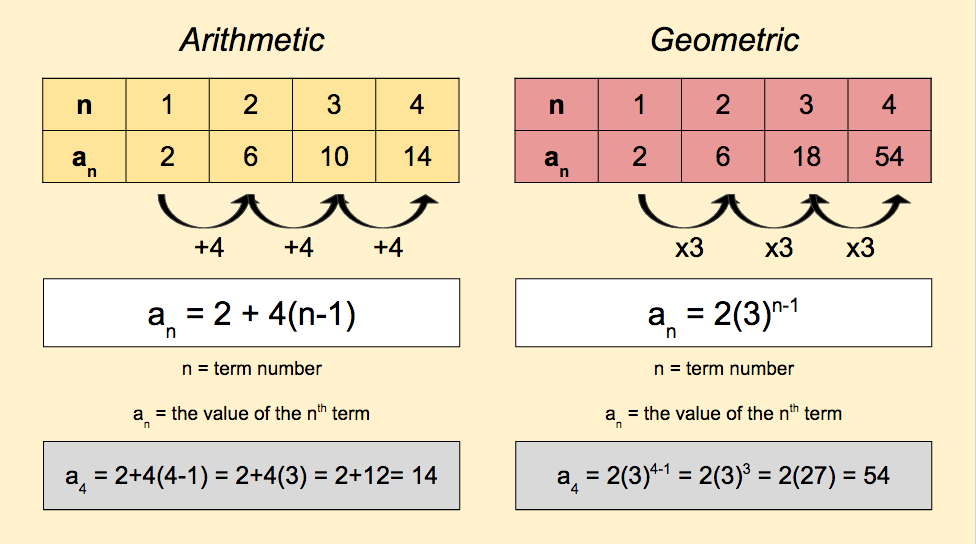
Arithmetic vs. Geometric Sequences
Click HERE to practice some work problems about arithmetic and geometric sequences!
Recursive Functions
Q2 Question Banks
| bank_exponentials1.pdf |
| bank_exponentials2.pdf |
| bank_sequences.pdf |